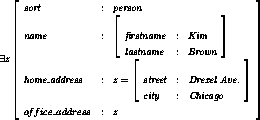
Figure 1.1: An example of a feature description. It can be interpreted as a person which works at home.
This thesis investigates the formal foundations of feature descriptions, which are partial descriptions, by means of functional attributes called features, of abstract record-like objects. Feature descriptions originated in the late seventies with so-called constraint-based grammars [Kay79,KB82,Shi86], a by now popular family of declarative grammar formalisms for the description and processing of natural language. More recently, the use of feature descriptions in constraint programming languages has been advocated and studied [AKN86,AKN89,AKP93,AKPS94,ST94]. Figure 1.1 gives an example of a feature description. One of the main operations defined on feature descriptions is unification, which takes two feature descriptions and yields either a failure, if the feature descriptions contain conflicting information, or a feature description that combines the information from both input descriptions.

Figure 1.1: An example of a feature description. It can be interpreted as a
person which works at home.
One of the main problems addressed in the literature is to provide an appropriate semantics for feature descriptions (and for various extensions of feature descriptions) as well as for the unification operation. There have been many diverging approaches to formalising feature descriptions (see sections 1.2 and 1.3). This thesis takes a clear position: following [Joh88,Smo88], we consider feature descriptions and their extensions as formulae in specific first-order languages. The semantics for feature descriptions is provided by a feature theory, which is a set of closed formulae (sentences) having at least one model. Unification is interpreted as an operation testing the satisfiability of conjunctions of feature descriptions.
In this thesis we will investigate several existing feature description
languages.
For the definition of the corresponding feature theories we apply
a standard first-order logic method which was used only recently
by [BS93a,AKPS94,ST94] in the
context of feature descriptions.
Given a feature
description language L, we interpret L over the fixed domain of
feature trees resulting in a first-order structure
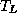 (henceforth called the standard interpretation of L). Then we take
the feature theory for L to be the set of sentences valid in
(henceforth called the standard interpretation of L). Then we take
the feature theory for L to be the set of sentences valid in
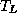 (called the theory of
(called the theory of 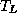 ).
This approach has the advantage that it is fairly intuitive.
Furthermore, it yields a complete theory (i.e., for every L-sentence
).
This approach has the advantage that it is fairly intuitive.
Furthermore, it yields a complete theory (i.e., for every L-sentence 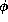 ,
either
,
either 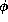 or
or 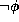 is contained in theory of
is contained in theory of 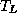 ).
).
Feature trees are trees where the edges are labelled by features and the
leaves are labelled by atoms. The labelling is
functional, that is, the direct subtrees of a feature tree are
uniquely determined by the features of the edges leading to them.
The names of features and atoms are taken out of a common infinite set of
labels 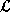 . Formally, a feature tree is a pair consisting of a
prefix-closed subset D of
. Formally, a feature tree is a pair consisting of a
prefix-closed subset D of 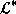 together with a total mapping
together with a total mapping
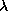 of the leaves of D (i.e., the set of elements p in D
with the property that there is no feature f pf is in D) into
of the leaves of D (i.e., the set of elements p in D
with the property that there is no feature f pf is in D) into
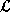 .
Examples of feature trees are listed in Figure 1.2.
The elements of
.
Examples of feature trees are listed in Figure 1.2.
The elements of 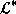 are called paths.
are called paths.
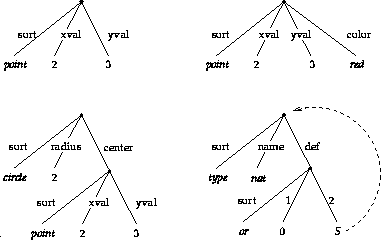
Figure 1.2: Examples of Feature Trees.
Our feature description languages are
first-order languages which do not contain proper function symbols, but
contain for every symbol of
 a corresponding constant symbol.
As described above, every language is associated with a standard interpretation
whose domain is the set of all feature trees. In this
interpretation,
the constant symbols are
interpreted as
atomic feature trees (i.e., as feature trees having no
subtrees).
In particular, we will consider the following languages (and their
corresponding standard interpretations) in this thesis:
a corresponding constant symbol.
As described above, every language is associated with a standard interpretation
whose domain is the set of all feature trees. In this
interpretation,
the constant symbols are
interpreted as
atomic feature trees (i.e., as feature trees having no
subtrees).
In particular, we will consider the following languages (and their
corresponding standard interpretations) in this thesis:
 , and for every symbol in
, and for every symbol in 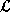 a binary relation symbol.
A feature constraint xfy with
a binary relation symbol.
A feature constraint xfy with 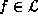 holds in the
standard interpretation of FT
iff y is the
subtree of x under the feature f, and
holds in the
standard interpretation of FT
iff y is the
subtree of x under the feature f, and
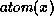 holds if x denotes an atomic feature tree.
This language was
introduced in [BS93a,AKPS94] with
minor differences and
contains the descriptional primitives used in every
feature description language. Hence, we call this language the
basic feature description language.
holds if x denotes an atomic feature tree.
This language was
introduced in [BS93a,AKPS94] with
minor differences and
contains the descriptional primitives used in every
feature description language. Hence, we call this language the
basic feature description language.
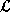 .
An arity constraint
.
An arity constraint 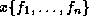 is true in the
standard interpretation of CFT
if x has
exactly
is true in the
standard interpretation of CFT
if x has
exactly 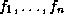 as features under its root. This language
permits the specification of complete information for some variable x by
specifying the arity of x and the subtrees of x under the
features listed in the arity of x. As we will show, this is not
possible in the
language of FT
(the feature descriptions in FT
are
inherently partial). CFT
was introduced in a slightly different form
by [ST94] and
combines the expressive power of FT
\
with Colmerauer's rational tree constraint system RT
for Prolog-II.
as features under its root. This language
permits the specification of complete information for some variable x by
specifying the arity of x and the subtrees of x under the
features listed in the arity of x. As we will show, this is not
possible in the
language of FT
(the feature descriptions in FT
are
inherently partial). CFT
was introduced in a slightly different form
by [ST94] and
combines the expressive power of FT
\
with Colmerauer's rational tree constraint system RT
for Prolog-II.
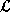 , a binary relation symbol. A regular path
expression
xLy holds in the standard interpretation of RFT
if y is the
subtree of x under some path p, where p is an element of the
regular set of paths denoted by L.
Using this language, it is now possible to specify properties of
arbitrarily deep subtrees, where the paths leading to
the subtrees can be restricted by a regular expression.
Regular path expressions were introduced as ``functional
uncertainty'' by [KZ88,KM88]
for handling long-distance phenomena
in the context of the grammar formalism LFG [KB82].
, a binary relation symbol. A regular path
expression
xLy holds in the standard interpretation of RFT
if y is the
subtree of x under some path p, where p is an element of the
regular set of paths denoted by L.
Using this language, it is now possible to specify properties of
arbitrarily deep subtrees, where the paths leading to
the subtrees can be restricted by a regular expression.
Regular path expressions were introduced as ``functional
uncertainty'' by [KZ88,KM88]
for handling long-distance phenomena
in the context of the grammar formalism LFG [KB82].
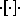 . A
generalised feature constraint
. A
generalised feature constraint 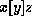 is true in the standard
interpretation of F
if y denotes an atomic feature tree and z is
the subtree of
x under the feature f, where f is the label of the atomic feature
tree denoted by y. In this language, features are now first class
objects (i.e., it is now possible to quantify over features).
Feature descriptions with first class features have been
considered in [Joh88,Tre93].
is true in the standard
interpretation of F
if y denotes an atomic feature tree and z is
the subtree of
x under the feature f, where f is the label of the atomic feature
tree denoted by y. In this language, features are now first class
objects (i.e., it is now possible to quantify over features).
Feature descriptions with first class features have been
considered in [Joh88,Tre93].
Note that for the basic feature description language FT , the literature has mainly employed a different standard interpretation (see [Smo88,Smo92]). The domain of this standard interpretation consists of feature graphs, which are directed, labelled graphs with edges labelled by features.
To obtain a well-investigated theory for these languages, we address the following questions in our thesis:
Concerning the question of the expressivity of feature description languages, only
minor results can be found in the literature, and they are (with a few
exceptions) stated only informally.
There does not even exist a fixed definition for the
expressivity of a feature description language. Using the
domain of feature trees for the interpretation of the feature
description languages, however, we obtain a simple definition of expressivity,
using a standard first-order technique.
The expressivity of a language L is defined as the set of relations on
feature trees that are definable by L-formulae. An n-ary
relation R over feature trees is said to be definable in L if there
is an L-formula
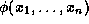 with
with 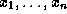 as free variables
the set of tuples of feature trees
as free variables
the set of tuples of feature trees
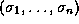 satisfying
satisfying 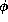 in the standard interpretation
in the standard interpretation
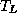 of L is exactly R.
Using this definition of expressivity,
we follow the work of [Tre93], who showed
that the languages
FT
and CFT
are less expressive than F
.
Note we can use such a simple definition of
expressivity since we interpret all the languages over
the same domain of feature trees. This is a strong indication that the
approach of defining a feature theory via a standard interpretation is fruitful
and should be carried over to other languages.
of L is exactly R.
Using this definition of expressivity,
we follow the work of [Tre93], who showed
that the languages
FT
and CFT
are less expressive than F
.
Note we can use such a simple definition of
expressivity since we interpret all the languages over
the same domain of feature trees. This is a strong indication that the
approach of defining a feature theory via a standard interpretation is fruitful
and should be carried over to other languages.