Chapter 2 defines the domain of feature trees
and some basic relations and functions on feature trees. We then
define the first-order languages F
, FT
, CFT
and RFT
,
and introduce the standard interpretations of these languages and
the corresponding substructures consisting only of the rational feature
trees.
Chapter 3 investigates the expressivity of our
universal feature description language F
. According to our definition
of expressivity, we present for every n-ary relation R over feature
trees, which is encodable in F
, a formula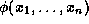 
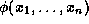(called explicit definition for R) whose
denotation in the standard interpretation is R.
Interestingly, we can use the same definitions if we restrict the
relations to the set of rational trees and replace the
standard interpretation by its substructure consisting only of the
rational feature trees.
Chapter 4 presents axiomatisations of the theories
of the standard interpretation of FT
and CFT
and proves their
completeness. We show that the feature graph
interpretation of FT
is also a model of the axiomatisation of the theory of FT
.
Furthermore, we show that FT
is really less expressive than CFT
.
Chapter 5 shows that the satisfiability problem for
conjunction of regular path expressions is decidable. Furthermore, we
show that the feature tree interpretation of RFT
is canonical for
satisfiability (i.e., a conjunction of regular path expressions of
satisfiable if and only if its is satisfiable in the feature tree
interpretation). Thus, the positive existential fragment of the theory
of RFT
is decidable.