
Feature descriptions are used in several constraint programming languages, where the main representatives are the languages LIFE [AKP93,AK93,MAK90], which is a constraint logic programming language with functions and inheritance, and Oz [HSW93,HSW95,Smo94a,Smo94c,Smo94b,Smo94d], which is a higher-order object-oriented concurrent constraint programming language. Others languages using feature descriptions are Le Fun [AKLN87,AKN89] and Login [AKN86].
The logical sublanguages of both LIFE and Oz are strongly influenced by the constraint logic programming scheme of Jaffar and Lassez [JL87]. In this scheme, Prolog's first-order constructor terms are replaced by a constraint system (i.e., a constraint language together with a class of interpretations), and the unification operation of Prolog is replaced by a satisfiability test of conjunctions of formulae in the constraint language. Höhfeld and Smolka [HS88] generalise the constraint logic programming scheme to definite specifications over arbitrary constraint languages. If the constraint language is closed under conjunction and renaming of the variables, then both the operational and declarative semantics can be defined in a uniform way.
Oz is also influenced by Saraswat's concurrent constraint programming scheme [SR90,Sar91]. To illustrate the principle of this scheme, we define concurrent agents to be expressions of the form

where 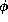 ,
, 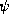 and
and 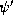 are formulae in the constraint
language.
are formulae in the constraint
language. 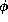 is called the guard of the agent. The agents live
in a context, which itself is just
another formula
is called the guard of the agent. The agents live
in a context, which itself is just
another formula 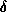 of the constraint language.
For reducing an agent in some context one has to test whether the
context entails or disentails the guard in the underlying constraint system.
A formula
of the constraint language.
For reducing an agent in some context one has to test whether the
context entails or disentails the guard in the underlying constraint system.
A formula 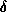 entails a formula
entails a formula 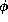 if in every interpretation of the constraint system, every valuation satisfying
if in every interpretation of the constraint system, every valuation satisfying
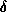 also satisfies
also satisfies 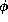 . If the context
. If the context 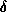 entails the guard
entails the guard
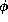 of the above agent, then
of the above agent, then 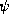 is conjoined to the
context. If
is conjoined to the
context. If 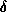 disentails
disentails 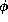 (i.e., entails
(i.e., entails 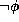 ),
then
),
then 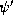 is conjoined to the context. Otherwise, the agent
is suspended. It will be reawoken if the evaluation of other
agents changes the context.
is conjoined to the context. Otherwise, the agent
is suspended. It will be reawoken if the evaluation of other
agents changes the context.
The main motivation for using feature descriptions in these languages is that they provide the notion of a record, familiar from programming languages such as Pascal, as a basic datatype, in a natural and flexible way. LIFE uses open records (i.e., records whose arity is not fixed), whereas Oz uses closed records with fixed arity. This is also reflected by the fact that the basic constraint language of LIFE is similar to FT , whereas Oz uses CFT as basic constraint language. Oz also incorporates extensions of CFT , but the evaluation of these additional constraints is delayed until enough information has been gathered to transform these constraints into corresponding CFT -constraints. Besides the satisfiability test on conjunctions of constraints (which is delayed in the case of Oz for efficiency reasons), the entailment test is another important operation used in these languages.
The flexibility of feature descriptions arises from the fact that
they allow for partial descriptions.
A good example for this flexibility is the language
CFT
, which combines the expressivity of FT
and RT
.
The following examples are taken from [ST94].
Given an RT
-formula 

we can translate  into the following equivalent CFT
-formula:
into the following equivalent CFT
-formula:
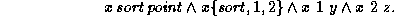
But CFT has more expressive power than RT . It is possible to express within CFT that a record has some feature without specifying others. A description of the form

just states that x has a colour feature, but it does not disallow other features such as shape, size or position. If the language has a finite signature, the description above can be defined in RT by a disjunction of the form
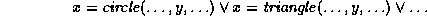
enumerating all constructors for which a colour feature is
appropriate. But the computational behaviour of this disjunction is much
worse than that of the single constraint  . In the
case of an infinite signature (which we consider here), such a
single feature constraint is not definable in RT
(since it
would correspond to an infinite disjunction).
. In the
case of an infinite signature (which we consider here), such a
single feature constraint is not definable in RT
(since it
would correspond to an infinite disjunction).