


Next: Feature Descriptions and
Up: Feature Descriptions in
Previous: Feature Descriptions in
Historically, the formal foundation for feature descriptions in
constraint programming languages started with the work of Hassan
Aït-Kaci [AK86], who introduced the 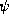 -term calculus.
-term calculus.
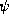 -terms are equivalence classes
of feature descriptions that are closed under consistent variable
renaming. Later, [Smo92] considered feature descriptions
as formulae in a first-order language and introduced feature graphs as
an interpretation for feature descriptions which is canonical for
satisfiability (i.e., a feature description is satisfiable if it is
satisfiable in the feature graph interpretation).
He also provided a translation of
Aït-Kaci
-terms are equivalence classes
of feature descriptions that are closed under consistent variable
renaming. Later, [Smo92] considered feature descriptions
as formulae in a first-order language and introduced feature graphs as
an interpretation for feature descriptions which is canonical for
satisfiability (i.e., a feature description is satisfiable if it is
satisfiable in the feature graph interpretation).
He also provided a translation of
Aït-Kaci 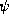 -terms into his language.
-terms into his language.
The languages FT
and CFT
were introduced
in [AKPS94] and [ST94], respectively.
Each defined the corresponding feature theory via an axiomatisation which is
very similar to the axiomatisation of the standard interpretation
of the language as presented
in this thesis (in fact, the axiomatisation
in [AKPS94] was taken from [BS93a]).
But they didn't address the problem of proving completeness of their
axiomatisations.
And each presented a decision
procedure for fragments of these theories, namely an incremental
algorithm for testing simultaneously
entailment and disentailment
of possibly existentially quantified conjunctions of constraints.
Since the class of interpretations of these languages are determined by
a theory, we can reformulate the notion of entailment.
A formula
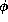 entails a formula
entails a formula 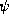 in some theory T (written
in some theory T (written 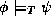 ) iff
) iff

and disentails 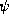 iff
iff

Furthermore, both prove the
independence property. A theory T satisfies the independence property
if for all formulae
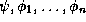 in the positive existential fragment of the
language of T,
in the positive existential fragment of the
language of T,
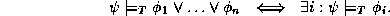
If a theory T satisfies the independence property, then an algorithm
for testing entailment and disentailment in T can be used for deciding
the existential fragment of T.
Since we can decide the full theories of FT
and CFT
, it is clear that
both the entailment and disentailment test can be
performed using our simplification algorithms for these theories.
But the ones in [AKPS94]
and [ST94] are more efficient since they are
optimised for this purpose. On the
other hand, these algorithm apply only to a very limited fragment.
A simple example that
is not covered by these algorithms is to
test whether

is entailed by
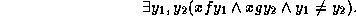
This can be decided using our simplifications algorithm.
The languages FT
and CFT
were introduced
in [AKPS94] and [ST94] with a
slightly different signature. Their signatures didn't contain the constant
symbols and the predicate symbol  , but used sort symbols instead.
Sorts are unary predicate symbols which are interpreted as disjoint sets.
Both also considered feature trees, which were defined slightly
differently because of the different signature. Their feature trees had
labels at every node (whereas our feature trees bear label only at the
leaves). The denotation of a sort symbol A in the feature tree
interpretation is exactly the set of all feature trees having the root
labelled with A. Their results can easily be adapted for our signature.
, but used sort symbols instead.
Sorts are unary predicate symbols which are interpreted as disjoint sets.
Both also considered feature trees, which were defined slightly
differently because of the different signature. Their feature trees had
labels at every node (whereas our feature trees bear label only at the
leaves). The denotation of a sort symbol A in the feature tree
interpretation is exactly the set of all feature trees having the root
labelled with A. Their results can easily be adapted for our signature.
We changed the signature in order to gain a bit more
expressivity. Sorts can be expressed in our languages by introducing
a new feature sort and a new constant symbol for each sort symbol, and by
replacing a sort constraint of the form Ax (in prefix notation) with the
constraint

In our signature, we can express the fact that two variables share the
same sort, without knowing the sort:
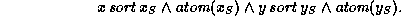
This implies that we have sorts as first class values, which is not true of
the signatures used
in [AKPS94,ST94].
A complete axiomatisation for Colmerauer's rational tree system RT
\
over an infinite signature was given in [Mah88].
Our completeness proofs for the languages FT
and CFT
have the same
overall structure used in [Mah88].
However, Maher's proof depends heavily on the
structure of first-order terms, since it uses substitutions. This is not
appropriate in our case since we are using a relational language.
A complete axiomatisation for RT
over a finite signature is
given in [Mah88,CL89].
A different completeness proof for CFT
is presented in [BT94],
where Ehrenfeucht-Fraïssé games are used. The method is semantic, in
showing that all models of CFT
are elementarily equivalent (i.e.,
make the same sentences valid), which immediately implies that CFT
\
is complete. This yields a trivial decision method for
CFT
-sentences, by enumerating all consequences of
CFT
. Given an arbitrary sentence  , the enumeration will
produce either
, the enumeration will
produce either 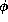 or
or 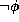 since CFT
is complete.
On the other hand, this thesis employs a proof theoretic
method in showing explicitly that for every sentence
since CFT
is complete.
On the other hand, this thesis employs a proof theoretic
method in showing explicitly that for every sentence 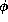 ,
either
,
either 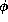 or
or 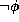 is valid in CFT
. Both methods have their
merits. The proof
in [BT94] is shorter (though similar problems arise in handling
inequations), while the proof in this thesis presents a decision method
for validity.
is valid in CFT
. Both methods have their
merits. The proof
in [BT94] is shorter (though similar problems arise in handling
inequations), while the proof in this thesis presents a decision method
for validity.
Another closely related work is the one by Treinen [Tre93],
who introduced the languages F
(again with sort symbols instead of
constants) and EF
, which is F
extended with arity constraints as used
in CFT
. Treinen also defined the
standard interpretation of feature trees for these languages.
Since arity constraints are definable in F
, the expressivity
of F
and EF
is the same. But this is only true if we consider the
full first-order theory. For the existential fragment, these theories
clearly differ. Treinen showed that the existential fragment of the theory of the
feature tree interpretation of EF
is decidable. Furthermore, he proved
that the full theory
of F
is undecidable. In contrast with our work, Treinen was not
concerned with showing that F
is a universal feature
description language.



Next: Feature Descriptions and
Up: Feature Descriptions in
Previous: Feature Descriptions in
Rolf Backofen
Thu Aug 3 14:08:12 MET DST 1995
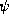 -term calculus.
-term calculus.
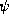 -terms are equivalence classes
of feature descriptions that are closed under consistent variable
renaming. Later, [Smo92] considered feature descriptions
as formulae in a first-order language and introduced feature graphs as
an interpretation for feature descriptions which is canonical for
satisfiability (i.e., a feature description is satisfiable if it is
satisfiable in the feature graph interpretation).
He also provided a translation of
Aït-Kaci
-terms are equivalence classes
of feature descriptions that are closed under consistent variable
renaming. Later, [Smo92] considered feature descriptions
as formulae in a first-order language and introduced feature graphs as
an interpretation for feature descriptions which is canonical for
satisfiability (i.e., a feature description is satisfiable if it is
satisfiable in the feature graph interpretation).
He also provided a translation of
Aït-Kaci 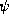 -terms into his language.
-terms into his language.
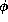 entails a formula
entails a formula 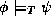 ) iff
) iff


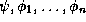 in the positive existential fragment of the
language of T,
in the positive existential fragment of the
language of T,
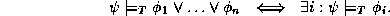

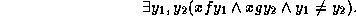
 , but used sort symbols instead.
Sorts are unary predicate symbols which are interpreted as disjoint sets.
Both also considered feature trees, which were defined slightly
differently because of the different signature. Their feature trees had
labels at every node (whereas our feature trees bear label only at the
leaves). The denotation of a sort symbol A in the feature tree
interpretation is exactly the set of all feature trees having the root
labelled with A. Their results can easily be adapted for our signature.
, but used sort symbols instead.
Sorts are unary predicate symbols which are interpreted as disjoint sets.
Both also considered feature trees, which were defined slightly
differently because of the different signature. Their feature trees had
labels at every node (whereas our feature trees bear label only at the
leaves). The denotation of a sort symbol A in the feature tree
interpretation is exactly the set of all feature trees having the root
labelled with A. Their results can easily be adapted for our signature.

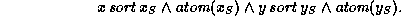
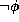 since CFT
is complete.
On the other hand, this thesis employs a proof theoretic
method in showing explicitly that for every sentence
since CFT
is complete.
On the other hand, this thesis employs a proof theoretic
method in showing explicitly that for every sentence