Feature Descriptions and Constraint-Based Grammars

In the last decade, a family of grammar formalisms has become popular which is subsumed under the term constraint-based grammar formalisms. These formalisms have in common that they use feature descriptions for modelling linguistic entities such as words, phrases and sentences. Some of the most widely used grammar models in formal theoretical linguistics such as LFG [KB82], FTAG [VSJ88] and HPSG [PS87] employ constraint-based formalisms. One of the main advantages of such formalisms is that they provide a declarative representation of linguistic knowledge, i.e. the linguistic knowledge can be stated independently from the way it is processed. This has important impact on grammar engineering in computational linguistics. For example, the time for developing a sizeable grammar in these formalisms is usually much less than in other formalisms. Because of the declarative semantics of the formalism, constraint-based grammars exhibit a higher potential for reusability (see for example [RJ94]).

For this reason, European-Union-funded projects involving grammar development have adopted constraint-based grammar formalisms [Eur94].

The motivation for using feature descriptions as representation formalism in constraint-based grammar formalism is stated in [PS87, page 7,]:

``In all these formalisms and theories, linguistic objects are analysed in terms of partial information structures which mutually constrain possible collections of phonological structure, syntactic structure, semantic content and contextual factors in actual linguistic situations. Such objects are in essence data structures which specify values for attributes; their capability to bear information of non-trivial complexity arises from their potential for recursive embedding ... and structure-sharing ....''

In the following, we give a detailed example of the use of feature descriptions in constraint-based grammars. We start with an example of annotated context-free rules (phrase structure rules) as used in the PATR-II [SUP83,Shi89,Shi92] or LFG [KB82] formalisms. These annotations further restrict the set of derivations that are licenced by some grammar rule. Figure 1.3 shows a small grammar for English. A rule of the form

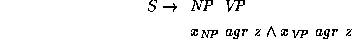
consists of the context-free rule 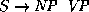, which is annotated by the feature description 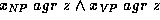, where , and are logical variables.

    
Figure 1.3: A small grammar

Derivations are described over annotated phrase structures. A phrase structure is a labelled, ordered tree. An annotated phrase structure consists of a phrase structure, a feature description and an association of the non-terminal nodes of the phrase structure with the free variables in the feature descriptions. We indicate that some non-terminal node of a phrase structure is associated with the variable by writing 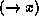to the right of this node. An example of an annotated phrase structure is

Here, Mary, loves and John are the terminal nodes. When a rule is applied to some leaf of an annotated phrase structure, then the phrase structure is expanded according to the context-free part of the grammar rule. The variable on the left-hand side of the rule is identified with the variable associated with the expanded node, and all other variables of this feature description are consistently renamed to new variables. The resulting feature description is added conjunctively to the feature description of the initial annotated phrase structure. Thus, applying the rule 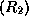to

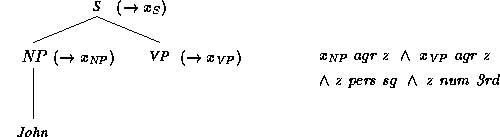
yields

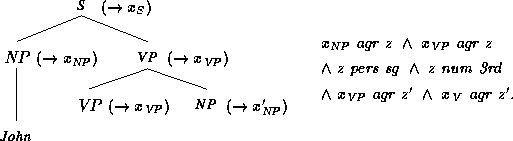
Note that the feature description associated with the result can be simplified to 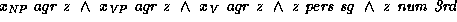. An annotated phrase structure is licenced by a grammar if it can be generated by applying the grammar rules as described above and if the associated feature description is satisfiable.

In some modern grammar formalisms, which are influenced by the work on of the grammar theory HPSG (Pollard and Sag [PS87,PS94]), a more radical approach is taken by uniformly representing all linguistic data (including the phrase structure) within feature descriptions. Since phrase structures are ordered trees, the ordering information must be represented explicity using lists of feature descriptions. A list of feature trees 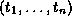can be represented as a feature tree using the features 11 and 22 and the atom nil :

The clumsiness of list description using this encoding can easily be avoided using some syntactic sugar. Thus, we write 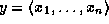for

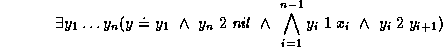
Using this representation of list, we can encode the information contained in an annotated phrase structure within feature descriptions. Here, we use the feature syn to denote the non-terminal symbol associated with the phrase structure, the feature phon to denote the string of terminals covered by the phrase structure, and the feature dtrs to list the phrase structures which occur directly under the root. Using this encoding, the annotated phrase structure

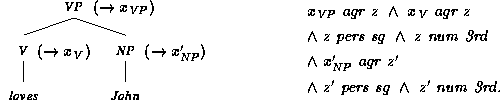
is translated into the following feature description (where we use matrix notation for better readability):

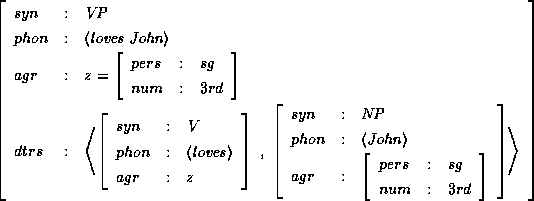
After the encoding of annotated phrase structure is established, the question arises as to how to transform the grammar listed in Figure 1.3. First note that we can read a grammar rule such as 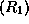as a recipe for building an annotated phrase structure with top-symbol 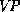, given phrase structures for a V and an 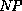. Conversely, we know that every phrase structure labelled with 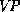must have a V followed by an 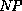since there is only one rule having 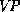at the lefthand side. This implies that the set of feature trees satisfying the feature descriptions of a verb phrase 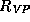can be described by the formula

where and 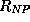are unary predicates denoting the feature trees representing 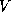s and 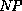s, respectively; 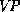is an atom symbol; and 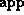is the append relation on the feature tree representation of lists as defined on page . Note that the definition for 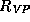is a definite equivalence.

Using this formalisation of grammatical rules, parsing (and if we had added semantics in our examples also generation) can ideally be described as a pure deductive process [Per83]. A sentence word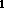 ... word is licenced by the grammar G if

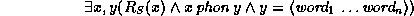
is valid in all models of G (or valid in some model of G, depending on the intended semantics of grammars).

In representations of grammatical rules (and/or grammatical principles; for a detailed discussion on the difference of grammatical rules and grammatical principles see [PS87]) like (1.2), the relation symbols representing linguistic entities (such as 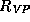etc.) are always unary predicates. Now there are quite a number of formalisations that are concerned with feature description languages that contain unary predicate symbols in their signatures. In these formalisations, the unary predicate symbols are called types, and the languages are called typed feature description languages. For example, both FT and CFT \ were introduced in [AKPS94] and [ST94] as typed feature description languages (where the unary predicate symbols were called sorts instead of types). But as the discussion in section 1.2 shows, these types can be simulated using constants, and our versions of FT and CFT are even more expressive.

Based on typed feature descriptions, the concept of type systems played an important in the literature on constraint-based grammar formalisms ([AK86,EZ90b,EZ90a,Pol89,PM90,Smo92,AKPG93,Car92,Zaj92,KS94]) since they allow for a direct encoding of grammatical principles as defined in the grammar theory HPSG [PS87,PS94]. A type system consists of a partial order on the type symbols defining type inheritance and a set of type definitions of the form

where T is a type symbol and 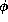is a typed feature description. The ordering is interpreted as the subset relation on the sets denoted by the types, and a type definition 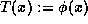restricts the denotation of T to the set of all elements x satisfying . But as [Bac95b] shows, type systems can be translated into definite equivalences, and the intended interpretation for type systems is the greatest model of the resulting set of definite equivalences. Retrospectively, one can say that the reason for concentrating on the unary predicate symbols (types) is that the unary predicates model classes of linguistic entities (which are the objects of main interest in constraint-based grammars). This focus might have been the reason that type systems and definite equivalences have often been considered as different concepts. For a detailed discussion of type systems, the interested reader is referred to [Kri95].

Many modern implementation of constraint-based grammar formalisms use type systems. Furthermore, nearly all implementations provide a mechanism whose semantics can be described in terms of definite equivalences.

In the following, we consider the systems ALE [Car92,Car94], TFS [Zaj92], CUF [DE91,DD93] and TDL / UDiNe [BK93,KS94], which is a representative selection of advanced constraint-based grammar formalisms (descriptions of these and other implemented systems can be found in [BKSU93]). Both TDL / UDiNe and TFS have type systems that allow for arbitrary type definitions, and grammatical principles can be defined via type definitions. In TFS , the constraint solver is built in and parsing (or generation) must be performed with the deductive system provided with the type system. Since in TDL / UDiNe the constraint-solver UDiNe is a separate component, it can also be used for efficiency reason together with a separated parser.

In ALE and CUF , the type systems allow only a restricted form of type definition, which is not sufficient for defining grammatical principles directly. Both systems instead provide a mechanism called definite clauses over feature description languages. The mechanism was introduced in [HS88] and generalises the constraint logic programming scheme of Jaffar and Lassez [JL87]. Definite clauses can be translated into a set of definite equivalences, where the intended semantics is the least model of the resulting set of definite equivalences [Smo93]. In CUF , these definite clauses can be used directly for defining grammatical principles, while this is not possible in ALE . The operational semantics used for the definite clauses in ALE is adapted from PROLOG, which is not the appropriate one for grammatical principles [Man93]. For this reasons, ALE has a built in parser for annotated context-free rules, in which grammatical principles can be specified.

Roughly speaking, the feature description languages used in the above-mentioned systems are syntactic variants of FT . Clearly, all systems handle the positive existential fragment of FT . Furthermore, negated equations are handled by ALE , TDL / UDiNe and CUF . UDiNe is (to our knowledge) the only implemented feature constraint solver which also handles negation of feature description as defined in [Smo92]. Given a conjunction of constraints 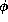and a distinguished variable x which is free in 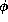, the negation of 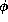with respect to the variable x is defined as

where X is the set of free variable of 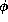. UDiNe additionally uses a syntactic variant of disjunction which appears in the literature under the name distributed disjunction ([Bac89,BEG90,DE89,DE90,MK89]). Distributed disjunction are disjunctions which bear an additional tag, a name. An example of a feature description with distributed disjunctions is

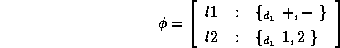
This feature description is equivalent to the disjunction of

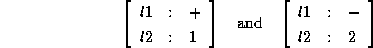
Note that the combinations

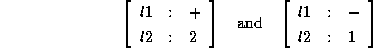
are not in the interpretation of . The advantages of distributed disjunctions are that they allow for a very compact encoding of linguistic data and that they often avoid expansion to disjunctive normal form during unification.

• Related Work