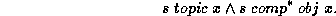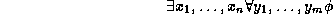
There have been many different and diverging formalisations for feature descriptions. Even for the basic feature description language which contains (roughly speaking) the descriptive primitives of FT , there have been many different approaches besides the predicate logic ones of [Joh88,Smo92]. Examples include the early work by Kasper and Rounds [RK86,KR86,KR90] using a non-standard logic, and the multi-modal logic approaches by [Rea91,BS93b] where every feature corresponds to a modal operator. At least these approaches are comparable to each other. But for the extensions to feature descriptions there are even more divergent approaches. Most of the formalisations were custom-built, and nearly every time a new extension to feature descriptions was proposed, a new formalisation was presented.
There was only one approach to building a more general feature theory (i.e., encoding different extensions in one single feature theory), namely that of Johnson [Joh91,Joh94], who used Schönfinkel-Bernays' formulae for the formalisation of feature descriptions. Schönfinkel-Bernays' formulae are of the form
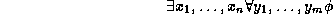
where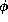 
is a quantifier-free formula. For this class of formulae,
the satisfiability problem is known to be decidable.
But this approach is restricted to decidable extensions of feature
descriptions, while we also want to encode undecidable extensions
such as definite equivalences. Furthermore, regular
path expression and subsumption constraints are not expressible within
the Schönfinkel-Bernays' fragment (see [Joh94, page 10,]),
although they are expressible in the feature description language F
.
Hence, no other feature description language presented in the literature
has an expressivity comparable to F
. For this reason, we call
F
a universal feature description language.
The notion of completeness as defined for FT and CFT \ is different from the notion of completeness considered in related work by Kasper and Rounds [KR90] and Moss [Mos92]. These authors study logical equivalence for rooted and quantifier-free feature descriptions and give complete equational axiomatisations of the respective congruence relations. In contrast, we are concerned with a much larger class of possibly quantified feature descriptions. Moreover, exploiting the power of predicate logic, we are not committed to any particular model or any particular deductive system, but instead prove a result that implies that any complete proof system for Predicate Logic will be complete for proving equivalence of feature descriptions any model of our feature theories for FT and CFT .
The complexity of the simplification algorithms is too high for use in a grammar formalism. But one could use the algorithms to decide general properties of a grammar, where the complexity is not relevant. For example, one can check with our simplification algorithms whether a grammatical rule is superfluous by virtue of being subsumed by another rule. For example, consider the two annotated context-free rules
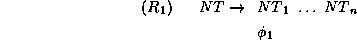
and
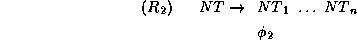
where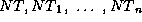 
are non-terminal
symbols 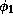and 
and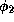 
are the annotated feature descriptions.
If 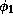entails 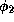(i.e., every valuation of satisfying
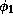also satisfies 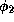), then 
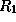is superfluous and can be
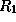removed, since in every derivation the application of rule can be
replaced by an application of rule 
. We have used annotated
context-free rules in this example for reasons of simplicity, but a similar
test can be performed for formalisms where the phrase structure is
encoded in feature descriptions. Now if the feature descriptions make
use of negated equations as in the example given in
section 1.2, page 
, the known
algorithm for testing entailment in FT
and CFT
\
(see [AKPS94] and [ST94], respectively)
cannot be used.
The use of such negated equation for constraint-based grammars is,
for example, considered in [Car92].
As mentioned, a partial result for the satisfiability problem of conjunction of regular path constraints was obtained in [KM88]. They showed that the satisfiability problem for conjunctive formulae containing regular path expression is decidable if an acyclicity condition is met. But it cannot be guaranteed that the acyclicity condition is maintained during the application of their algorithm for testing satisfiability.
Solving the satisfiability problem for cyclic descriptions containing regular path expressions requires a non-trivial extension of the algorithm described in [KM88]. Their algorithm uses a set of simplification rules that transforms a feature description into a normal form, from which satisfiability can be read off trivially. If the acyclicity condition is met, the rule system is terminating. But in the case of cyclic descriptions, termination cannot be guaranteed anymore. This is inherent to the problem. We solved the problem in this thesis by introducing a quasi-terminating rule system (see [Der87]). A rule system is quasi-terminating if it is not terminating, but produces only finitely many different results. To achieve a quasi-terminating rule system we had to translate the problem into a new syntax that enabled us to delay subproblems whose evaluation would cause an infinite number of results.
To see some possible application of regular path expressions, we briefly recall an example that is given in Kaplan and Maxwell [KM88, page 1,]. Consider the topicalized sentence
Using s as a variable denoting the whole sentence, the LFG-like clause
specifies
that in s, Mary should be interpreted as the object of the
relation telephoned. The sentence could be extended by
introducing additional complement predicates, e.g. in
sentences like Mary, John claimed that Bill telephoned; Mary, John
claimed that Bill said that ... Henry telephoned yesterday; ....
For this family of sentences the clauses
, 
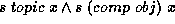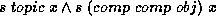and
so on would be appropriate; specifying all
possibilities would yield an infinite disjunction. This changes if
we make use of regular path expressions, allowing the above to be specified as the
single clause
