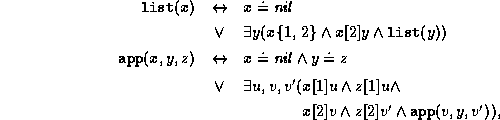The main results of the thesis are the following:
A particularly important class of relations are those
that can be described using definite equivalences over F
.
Definite equivalences
over arbitrary constraint languages are introduced
in [Smo93] and provide a machinery for defining
all recursive relations.
Given a set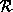 
of relation symbols that are not part of the signature
of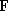 
, an equivalence
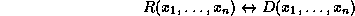
with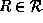 
is called definite if D
has at most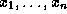 
as free variables and D is an
element of the class of all formulae
generated by the production rule
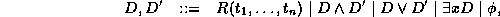
where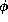 
denotes a F
-formula.
The following definition of
a feature tree representation of lists and the corresponding append
relation is
an example
of a set of definite equivalences:
A model of a set of definite equivalences is an interpretation of the extended language which is a conservative extension of the standard interpretation of F and which satisfies the equivalences. Note that a set of definite equivalences does not necessarily define a unique model, but there always exists a least and a greatest model (see [Smo93]). In the above example, the interpretation of list in the least model contains all representations of finite lists, whereas in the greatest model the representations of cyclic and infinite lists are also included.
Definite equivalences are important since they allow to define relations in the way they are defined by logic programs. A set of definite clauses P can be translated into an equivalent set of definite equivalences [Cla78,Smo93], whose least model is the model of P defined by the operational semantics of logic programming. Furthermore, type systems as used for processing modern constraint-based grammars can be translated into definite equivalences [Bac95b]. Here, both the least and the greatest model are viewed as the intended semantics.
In general, adding the concept of definite equivalences to a given language L enlarges the expressivity of L. We show in this thesis that F is expressive enough even to encode relations definable by the least model of a set of definite equivalences, and, under certain conditions, also the ones definable by the greatest model. Note that no feature description language having this expressivity was previously known. Since most of the relations used in applications are definable via definite equivalences, this implies that F is a universal feature description language.
Furthermore, we show that the feature graph interpretation of FT is also a model of the FT -axiomatisation. Since all models of a complete theory are elementarily equivalent, this implies that for the basic feature description language FT both the feature tree and the feature graph interpretation yield the same theory.
We will show that the theories of the feature tree interpretation and the
feature graph interpretation of CFT
differ.
As [ST94] stated,
one can translate every formula 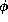in Colmerauer's rational tree constraint
system RT
into a CFT
-formula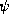 
such 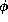is valid in the tree
interpretation of RT
(the standard interpretation of RT
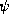) iff is
valid in feature tree interpretation of CFT
. This does not hold for the
feature graph interpretation of CFT
.
Our completeness proofs will exhibit simplification algorithms for the
theories of FT
and CFT
that compute for every feature description an equivalent solved form
from which the solutions of the description can be read off easily. For
a closed feature description the solved form is either 
(which
means that the description is valid) or 
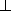(which means that the
description is invalid). For a feature description with free variables
the solved form is 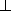if and only if the description is
unsatisfiable. As a by-product, we can use the existence of the solved
form to investigate the
properties of the theories. Thus, we can show that FT
is
really less expressive than CFT
, which is also a new result.
These results are partially published in [BS93a] and [Bac95a].
93] showed that this problem becomes
undecidable if we add unrestricted negation.
It has, however, remained an open problem as to whether satisfiability
of conjunctions of regular path expressions is decidable in the absence
of additional conditions (such as acyclicity). We will show that this is
indeed decidable, and furthermore, that the feature
tree model of RFT
is canonical for satisfiability (i.e., a conjunction of
regular path expressions is satisfiable if it is satisfiable in the
standard model of RFT
). This implies that the
positive existential fragment of the theory of the standard
interpretation of RFT
is decidable.
Even for the fragment of non-cyclic formulae, our algorithm is an improvement over the algorithm given in [KM88] since it allows for more flexible control in delaying the evaluation of complex regular path expressions. As [KM88] stated, delaying the evaluation of regular path expressions is an important method of gaining efficiency.
This result is partially published in [Bac94].
