antaRNA - Terrain Vertices and Edges Features
The antaRNA specific terrain is assembled from directed and weighted edges and
emitting vertex and one start vertex, which is non-emittant.
Vertices
Start Vertices
The start vertex is the origin of an ants travel through the graph. The Start
Vertex does not emit a nucleotide character. Its edges lead to the first emitting
vertex.

Emiting Vertices
Emiting vertices, if visited by an ant, emit one vertex specific nucleotide σ
to the ith position of the sequence. Its edges lead away to all vertices of
position j = i+1. In antaRNA, σ resembles a character from the RNA alphabet Σ = {A,C,G,U}.

Edges
An edge is directed, weighted, has a GC specific length and connects two vertices,
where one vertex is located at position i and the the other one at position j = i+1.
The weight resembles pheromonic information τ. The specific GC length η is
dependent of the nucleotide character of the resp. vertex in j and the requested GC content.
$e(i\sigma, j\sigma') = (\eta, \tau)$
The probability of an edge depends of all edged which lead away from a certain node.
For the calculation of the probability, the weighted information of a specific edge is set
into relation with all its competitive edges, such that a ant will randomly select an edge, based on
specific probabilities.
$
p(e_{(i\sigma,j\sigma')}) =
\frac{\alpha*\tau(e_{(i\sigma,j\sigma')})
+ \beta*\eta(e_{(i\sigma,j \sigma')})
}{\sum_{\sigma^{\ast} \in \Sigma} \left(
\alpha*\tau(e_{(i\sigma,j\sigma^{\ast})})+
\beta*\eta(e_{(i\sigma,j\sigma^{\ast})}) \right)}
$
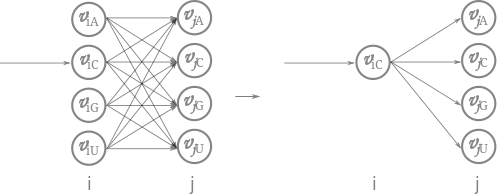
Situation at position i and j = i+1 wihtion the terrain. All vertices of i are connected to all vertices of j.
Lets say, an ant has chosen to visit vertex C at position i. This leads to the following situation:
Robert Kleinkauf 05/2015


